Informationssystemsystem Johanneum Lüneburg Dr. Dörte Haftendorn
Chaos und Fraktale		 Alphabetischer Index unten
Informationssystem
Mathematik  Chaos  Wegfraktale  Galerie  

Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten

hierhinDie Kochkurve,

ein ganz besonderes Wegfraktal und L-System

Sie kann als Symbol für diese ganze Fraktalgattung gelten. Der Mathematiker Helge von Koch hat sie zu Beginn des 20. Jahrhunderts vorgestellt.

Kochkurve stufenweise Dimension LOGO nahGalerie der Wegfraktale
Schneefockenkurve Didaktik L-System nahLeitseite der Wegfraktale





koch 2 koch 1 koch 0
Initiator ist der gerade Strich.
Generator ist eine 60°-Zacke.


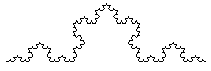
koch 5 koch 4 koch 3
So ensteht stufenweise ein immer vielfältiger verzweigtes Bild. Dabei werden kleinsten geraden Wege immer kleiner. Bei der Kochkurve ist der Verkleinerungsfaktor 1/3. Dadurch gelangt man recht bald an die Grenzen der Darstellbarkeit. Das mathematische Fraktal , die Kochkurve, ist die Grenzfigur dieses Prozesses. Man kann das Fraktal denken, sehen kann immer nur Vorstufen.
 Die Kochkurve ist streng selbstähnlich, d.h. man kann sie aus z=4 Bausteinen aufgebaut denken, wobei jeder dieser Bausteine mit dem Steckfaktor k=3 gesteckt werden muß um die selbst die Gestalt der ganzen Kochkurve anzunehmen.
Damit ist die nahSelbstähnlichkeitsdimension der Kochkurve d = log(z) / log(k) = log 4 / log 3 = 1,26. Man kann sie auch experimentell bestimmen durch nahMessung der Boxdimension hoch hierhin

Koch-Schnee Koch-Schnee Drei Exemplare der Kochkurve im gleichseitigen Dreieck angeordnet ergeben die kochsche Schneeflockenkurve. Sie ist ein wunderschöner Einstieg in dieses Thema. Kenner haben die Schneeflockenkurve nun schon so oft gesehen, dass sie gern eine Abwechslung hätten. Das gilt jedoch nicht für Schüler und andere Unerfahrene. Gerade die Dreiecksform, die dann Stufe für Stufe der Schneeflocke immer ähnlicher wird, ist leicht zu erfassen. Insbesondere steht unmittelbar vor Augen, dass auf endlichem Platz eine unendlich lange Kurve untergebracht wird.

Realisierung von Hand:
Einige Stufen können recht gut freihand gezeichnet werden und das sollte man auch wirklich tun. Danach ist es am am besten, einen Computer oder Bilder zur Verfügung haben. Besonders eindrucksvoll ist, wenn bei verlangsamten Computer der Aufbau des Bildes noch zu verfolgen ist.

Oben hoch hierhin

Realisierung mit rekursiven Prozeduren in nah LOGO 

PR koch :n :breite
   wenn :n =0  dann vw :breite rk
   koch :n-1 :breite / 3
   li 60
   koch :n-1 :breite / 3
   re 120
   koch :n-1 :breite / 3
   li 60
   koch :n-1 :breite / 3
 ENDE

Die Schneeflocke wird dann so verwirklicht:
bild re 30 koch 4 150 re 120 koch 4 150 re 120 koch 4 150

Oben hoch hierhin

Realisierung mit rekursiver Turtlegraphik-Prozedur in Pascal
Näheres zu Turtlegraphik in Pascal steht auf der Leitseite. 

Procedure koch ( stufe : integer );
             begin if stufe=1 then begin
                         fd(a);lt(60);fd(a);rt(120);
		 fd(a);lt(60);fd(a); end
                       else begin koch(stufe-1);lt(60);koch(stufe-1);
		   rt(120);koch(stufe-1);lt(60);koch(stufe-1); end;
	end;{proc}

Realisierung mit Lindenmayer-Systemen

    Kochkurve

  1. Das Axiom F (Stufe 0).
  2. Die Ersetzungregel ist F F+F--F+F (Stufe 1).
  3. In Stufe 2 ist dann F+F - - F+F+ F+F - - F - - F+F - - F + F+F - - F+F entstanden.
  4. Für Stufe 3 ist wieder jedes F mit der Ersetzungsregel zu ersetzen, u.s.w. .

nahSelbstähnlichkeitsdimension nahGalerie der Wegfraktale nahLeitseite Wegfraktale
Chaos und Fraktale jetzt neu nur bei Mathematik-Verstehen an der LEUPHANA Uni Lüneburg
Dort steht alles, was Sie hier sehen in neuer Gliederung mit deutlich weitergeführten Inhalten



obenAutor: © [Dr. Dörte Haftendorn]  Datum März 97. Letzte Änderung am 29. April 2007
Informationssystem [Fächer] [Mathematik] [Chaos] [Wegfraktale] [Galerie] [Webteam] [] Schulentwicklung